Pesawat Sederhana: Tuas, Bidang Miring, dan Katrol

Bahasan mengenai pesawat sederhana yang terdiri dari tuas atau pengungkit, bidang miring, dan katrol yang mencakup jenis, persamaan, dan keuntungan mekaniknya.

Halo Sahabat Gurnulis. Penulis kembali mengetengahkan artikel dengan topik materi pembelajaran ya. Kalau sebelumnya penulis membahas tentang perubahan energi, maka kali ini penulis hendak membahas pesawat sederhana. Pesawat sederhana ini terdiri dari tuas atau pengungkit, bidang miring, dan katrol. Yuk, sama kita simak.

Pengertian Pesawat Sederhana

Pesawat sederhana adalah alat yang digunakan untuk memudahkan atau meringankan pekerjaan. Ditinjau dari energinya, pada saat kita memindahkan suatu benda dengan memanfaatkan atau tidak memanfaatkan pesawat sederhana sebenarnya besarnya sama. Tetapi dengan menggunakan pesawat sederhana menjadi lebih ringan atau lebih mudah.

Pesawat sederhana terdiri dari:

1. tuas atau pengungkit;
2. bidang miring;
3. katrol.
   

Berikut bahasan dari ketiganya.

Tuas atau Pengungkit

Perhatikan gambar berikut!

 
Berdasarkan gambar di atas, tuas nomor berapakah yang menunjukkan keadaan setimbang? Tuas nomor berapakah yang menunjukkan keadaan tidak setimbang? Apa yang menyebabkan keadaan tuas tersebut? Berikut bahasan untuk untuk memahaminya.

 

Tuas (1) dalam keadaan setimbang. Keadaan setimbang pada tuas (1) disebabkan panjang lengan tuas yaitu l₁ = l₂ benda yang digantungkan pada kedua lengannya sama. Hal itulah yang menyebabkan tuas (1) menjadi setimbang.

 

Tuas (2) dalam keadaan tidak setimbang. Keadaan tidak setimbang pada tuas (2) disebabkan panjang lengan tuas l₁ < l₂ sedangkan berat benda yang digantungkan pada kedua lengannya sama. Hal itulah yang menyebabkan tuas (2) menjadi tidak setimbang.

 

Tuas (3) dalam keadaan setimbang. Keadaan setimbang pada tuas (3) disebabkan walaupun panjang lengan tuas l₁ < l₂ tetapi berat  benda yang digantungkan pada kedua lengannya berbeda. Jika kita perhatikan beban yang digantung pada lengan tuas l₁ besar sedangkan beban yang digantung pada lengan tuas l₂ lebih kecil. Hal itulah yang menyebabkan tuas (3) menjadi setimbang.
 

Rumus Persamaan Tuas atau Pengungkit

Untuk memudahkan pemahaman terhadap tuas atau pengungkit, kita dapat menuliskan persamaan yang berlaku pada tuas atau pengungkit sebagai berikut.

 

Secara matematis persamaan tuas yang berlaku pada gambar di atas dapat dinyatakan dengan persamaan sebagai berikut.

W x  l₁ = F x l₂

Keterangan:

W	= berat benda
F	= gaya
l1	= lengan beban
l2	= lengan kuasa

 

Rumus Keuntungan Mekanik Tuas atau Pengungkit

Pengungkit atau tuas dimanfaatkan oleh manusia untuk memindahkan benda yang berat dengan menggunakan gaya yang kecil. Tingkat kemudahan sebuah tuas atau pengungkit dinamakan dengan keuntungan mekanik.

 

Keuntungan mekanik tuas atau pengungkit dinyatakan dengan rumus berikut.

KM = W/F

KM = l₁/l₂

Keterangan:

W	= berat benda
F	= gaya
l1	= lengan beban
l2	= lengan kuasa

 

Contoh Soal Tuas atau Pengungkit

Perhatikan gambar berikut!

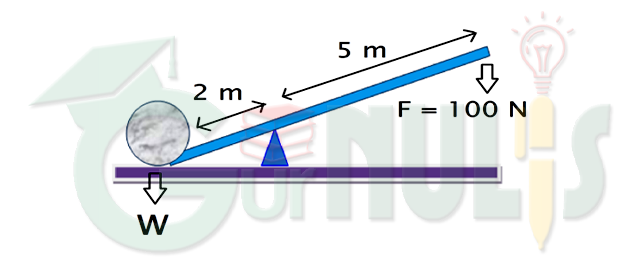
Sebuah tuas memiliki lengan kuasa sepanjang 5 meter dan lengan beban sepanjang 2 meter. Gaya yang diberikan pada lengan kuasa adalah sebesear 100 newton. Tentukan:

• berat beban;
• keuntungan mekanik.
  

Jawaban:

Menghitung berat beban.

W x l2	=   F x l2
W x 2	=   100 x 5
2W	=   500
W	=   500/2
W	=   250 newton.

 

Menghitung keuntungan mekanik.

KM	=   W/F
	=   250/100
	=   2,5 kali.

 

Jenis-jenis Tuas atau Pengungkit

Berdasarkan prinsip kerja tuas atau pengungkit manusia membuat berbagai alat yang dapat digunakan untuk memudahkan suatu pekerjaan. Beberapa alat tersebut antara lain tang, gunting, pemotong kuku, pemecah kemiri, pembuka botol, gerobak dorong, crane, dan sebagainya. Adapun gambar dari alat-alat yang menggunakan prinsip kerja tuas atau pengungkit ditunjukkan oleh gambar berikut ini.

 

Jenis-jenis tuas atau pengungkit adalah sebagai berikut.

• Tuas atau pengungkit golongan I. Tuas atau pengungkit golongan I di tengah-tengahnya adalah titik tumpu, dengan urutan kuasa - titik tumpu - beban. Contoh tuas atau pengungkit golongan I ini adalah gunting, penjepit rambut, tang, catut, penjepit kertas, palu (dalam fungsi mencabut paku), dan pencepit aki.
• Tuas atau pengungkit golongan II. Tuas atau pengungkit golongan II di tengah-tengahnya adalah beban, dengan urutan kuasa - beban - titik tumpu. Contoh tuas atau pengungkit golongan II ini adalah tang crimping, pemecah buah kemiri, pemotong kertas, pembuka tutup botol, handle rem, dan kereta barang roda satu.
• Tuas atau pengungkit golongan III. Tuas atau pengungkit golongan III di tengah-tengahnya adalah kuasa, dengan urutan beban - kuasa - titik tumpu. Contoh tuas atau pengungkit golongan III ini adalah cangkul, sekop, pinset, staples, dan pencapit gorengan.
  

 

Bidang Miring

Bidang miring adalah adalah alat yang dalam penggunaannya memindahkan suatu benda dengan memanfaatkan bidang yang dimiringkan. Cara memanfaatkan bidang miring sama seperti pengungkit, tetapi untuk memindahkan bendanya dengan cara menggeser ataupun mendorong diatas bidang miring tersebut.

Besar kecilnya gaya yang digunakan pada bidang miring sangat tergantung pada bidang miring yang digunakan. Untuk memindahkan sebuah benda dengan menggunakan bidang miring, gaya yang dikeluarkan menjadi besar jika bidang miringnya curam, dan gaya yang dikeluarkan menjadi kecil jika bidang miringnya semakin landai.
 

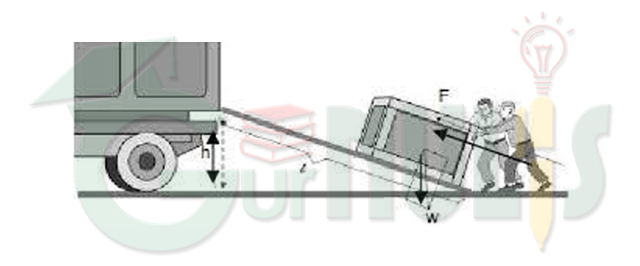
Rumus Persamaan Bidang Miring

Berdasarkan gambar di atas, persamaan yang berlaku dalam bidang miring dapat dinyatakan sebagai berikut.

F/W = h/s

dan

F = W x h/s

karena W = m.g

maka

F = m.g.h/s

Keterangan:

F	=   gaya
W	=   berat benda
m	=   massa
g	=   percepatan gravitasi
h	=   ketinggian bidang miring
s	=   panjang lintasan bidang miring

Rumus Keuntungan Mekanik Bidang Miring

Dengan menggunakan bidang miring, kita merasa akan lebih mudah atau lebih ringan untuk melakukan suatu kerja. Tingkat kemudahan yang diperoleh saat menggunakan suatu pesawat sederhana dinamakan keuntungan mekanik. Secara matematis keuntungan mekanik bidang miring dapat dinyatakan dengan rumus berikut.

KM	=   W/F
	=   s/h

Contoh peralatan yang menggunakan prinsip bidang miring adalah kapak, pahat, paku ulir, baut, paku, dan pisau. Perhatikan gambar berikut!

Contoh Soal Bidang Miring

Sebuah drum yang beratnya 6000 newton akan dinaikkan ke suatu tempat yang tingginya 2 meter dengan menggunakan bidang miring. Jika panjang lintasan bidang miringnya 5 meter, tentukan:

• gaya untuk memindahkan drum;
• keuntungan mekanik bidang miring yang didapatkan.
  

Jawab.

KM	=   s/h
	=   5/2
	=   2,5 kali
KM	=   W/F
2,5	=   6000/F
F	=   6000/2,5
F	=   2400 newton

 

Katrol

Salah satu jenis pesawat sederhana yang paling sering digunakan dalam kehidupan sehari-hari adalah katrol. Katrol bekerja seagaimana bidang miring dan tuas atau pengungkit, dapat digunakan untuk mengangkat benda dari suatu tempat ke tempat lain yang lebih tinggi.

 

Katrol dapat digunakan untuk mengubah arah gerak, berarti katrol tidak selalu menghasilkan keuntungan mekanik. Besar-kecilnya gaya yang diperlukan untuk mengangkat beban dengan menggunakan katrol sangat bergantung pada bagaimana cara merangkaikan katrolnya. Beberapa cara merangkaikan katrol sebagai pesawat sederhana ditunjukkan oleh gambar berikut.

Jenis-jenis Katrol

Katrol terdiri dari katrol tunggal tetap, katrol tunggal bebas, dan katrol majemuk. Berikut penjelasannya.

Katrol Tunggal Tetap

Pemanfaatan katrol tunggal tetap sering kita temukan untuk menimba air dari dalam sumur. Perhatikan gambar berikut.

Penggunaan katrol untuk menimba air sebenarnya tidak mendapatkan keuntungan mekanik, tetapi untuk mengubah arah gaya. Gaya yang diberikan pada tali katrol ke arah bawah sedangkan ember berisi air ke arah atas. Cara yang sama terjadi pada katrol yang digunakan untuk menaikkan bendera.

Berdasarkan gambar di atas, persamaan yang berlaku pada katrol tunggal tetap dapat dinyatakan sebagai berikut

W x l_b = F x l_k

 

dan

 

KM = W/F = l_b/l_k

Keterangan:

W	=   berat beban
F	=   gaya
lb	=   lengan beban
lk	=   lengan kuasa
KM	=   keuntungan mekanik

 

Katrol Tunggal Bebas

Katrol bebas atau katrol tunggal bergerak adalah katrol yang dapat bergerak bebas baik ke arah atas maupun ke arah bawah. Katrol tunggal bebas biasanya digunakan untuk mengangkat benda dan sekaligus dapat menggeser benda tersebut.  

Berdasarkan gambar tersebut, hubungan yang berlaku pada katrol tunggal bebas atau katrol tunggal  bergerak dapat dinyatakan dengan persamaan sebagai berikut

F x l_k = W x l_b

 

dan

 

KM = W/F = l_b/l_k

Keterangan:

W	=   berat beban
F	=   gaya
lb	=   lengan beban
lk	=   lengan kuasa
KM	=   keuntungan mekanik

 

Katrol Majemuk

Katrol majemuk dapat disusun dengan cara menggabungkan satu katrol tetap dengan beberapa buah katrol sehingga terbentuk satu kesatuan  sistem katrol yang baru. Gabungan katrol majemuk dapat berupa satu katrol tunggal tetap dengan satu katrol ganda, gabungan dua katrol ganda, atau lebih dari dua katrol ganda.

 

Tujuan dibuatnya katrol majemuk adalah untuk memperoleh keuntungan mekanik yang lebih besar dibandingkan dengan kedua jenis katrol tunggal di atas.

 

Berdasarkan percobaan yang telah dilakukan oleh para ahli fisika ternyata besarnya keuntungan mekanik pada katrol majemuk dapat ditentukan cara menghitung banyaknya tali yang menopang beban. Dengan kata lain keuntungan mekanik dipengaruhi oleh banyaknya jumlah tali yang menopang beban sesuai dengan katrol majemuk yang dibuat.

 

Ada beberapa hal yang perlu diperhatikan pada saat menentukan jumlah tali yang menopang beban pada katrol majemuk; yaitu:

• gaya pada tali yang arah tarikannya ke atas, dihitung juga sebagai keuntungan mekanik;
• gaya pada tali yang tarikannya ke bawah, tidak dihitung sebagai keuntungan mekanik.
  

 

Perhatikan gambar berikut! 

 

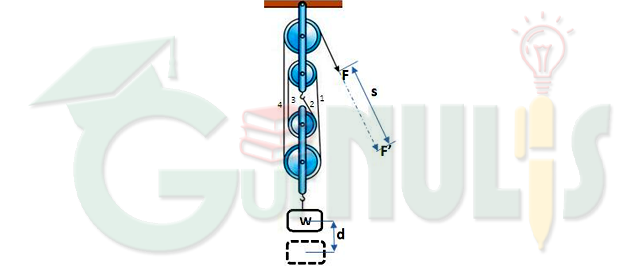
Jika kita anggap berat katrol-katrol dan talinya dapat diabaikan, berdasarkan gambar di atas, kita dapat menuliskan persamaan matematis yang berlaku pada katrol majemuk sebagai berikut.

 

Jumlah tali = 4, jadi keuntungan mekaniknya adalah

KM	=   4
	=   W/F
	=   s/d

Jika kita cermati pada kegiatan eksperimen katrol majemuk, ternyata gaya yang terukur pada dinamometer selalu lebih kecil jika dibandingkan dengan berat bebannya. Tetapi jika jarak pergeseran beban kita perhatikan, ternyata pergeseran beban selalu lebih kecil jika dibandingkan dengan pergeseran gayanya. Artinya usaha atau kerja pada lengan gaya dan usaha beban besarnya selalu sama. 

Kesimpulan

Sebenarnya dalam keadaan ideal penggunaan pesawat sederhana sama sekali tidak ada pengurangan usaha atau kerja. Gaya yang diberikan memang menjadi kecil namun akan selalu diikuti dengan semakin panjangnya jarak yang harus ditempuh. Jika gayanya ½ berat bebannya, jarak lintasannya menjadi 2 kali pergeseran bebannya.
 

Sifat semua pesawat sederhana, usaha atau kerja yang dilakukan untuk memindahkan beban dengan menggunakan pesawat sederhana selalu sama dengan usaha atau kerja yang dilakukan untuk memindahkan beban tanpa menggunakan pesawat sederhana.

Demikianlah bahasan mengenai pesawat sederhana yang terdiri dari tuas atau pengungkit, bidang miring, dan katrol ya Sahabat Gurnulis. Semoga bermanfaat.

Salam litersi guru ndeso.

Munasifatut Thoifah

Guru yang selalu ingin berbagi inspirasi.

Bagikan Artikel ini