Operasi Penjumlahan pada Bilangan Cacah

Bahasan mengenai operasi penjumlahan pada bilangan cacah yang dapat dibelajarkan melalui kumpulan, pengukuran, mesin fungsi, dan cara bersusun. Sifat penjumlahan pada bilangan cacah terdiri dari sifat tertutup dan sifat pertukaran.

Halo Sahabat Gurnulis, sebelumnya penulis telah membahas pengertian bilangan cacah dan sifat-sifatnya ya. Penulis ingin mengingatkan kembali pengertian dari bilangan cacah. Bilangan cacah adalah bilangan yang terdiri dari bilangan asli dan ditambah dengan nol (0). Pada artikel kali ini penulis masih hendak mengulas mengenai materi pembelajaran. Ini berkaitan dengan kompetensi pedagogik kita sebagai pendidik ya. Fokus penulis kali ini adalah operasi penjumlahan pada bilangan cacah.

Operasi penjumlahan adalah pengerjaan hitung yang pertama kali dikenal anak-anak. Bukan saja dikenal di sekolah, tetapi juga di masyarakat sebelum anak-anak mengenal sekolah. Hal-hal seperti ini bisa saja terjadi di lapangan, di warung, ataupun di tempat bermain, misalnya sebagai berikut.

Di lapangan ada 3 ekor sapi yang digembalakan, kemudian Budi membawa 2 ekor lagi. Berapa ekor sapi yang ada di lapangan sekarang?
Di rumahnya, Ibu Cantika mempunyai 1 butir telur. Ia pergi ke warung untuk membeli 3 butir telur lagi. Berapa butir telur yang ada di rumah Ibu Cantika sekarang?
Ada 2 orang anak sedang bermain di tempat bermain. Tidak berapa lama, datang temannya 4 orang bergabung. Berapa anak yang sekarang ada di tempat bermain?

Itulah sebagian contoh persoalan hidup sehari-hari yang penyelesaiannya memerlukan pemahaman mengenai operasi penjumlahan, terutama penjumlahan bilangan cacah.

Fakta-fakta Dasar Penjumlahan Bilangan Cacah

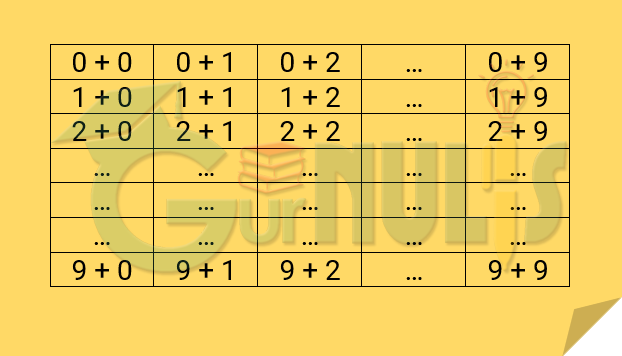
Di sini yang penulis maksud sebagai fakta-fakta dasar penjumlahan adalah penjumlahan atau kombinasi bilangan dari 0 sampai dengan 9, misalnya 9 + 1, 6 + 3, ataupun 9 + 9. Adapun 12 + 9 bukanlah fakta dasar penjumlahan, karena 12 bukanlah bilangan yang lambangnya terdiri dari satu angka. Fakta dasar penjumlahan ada 100 kombinasi, yaitu sebagai berikut.

Dari gambar di atas dapat dilihat bahwa fakta dasar penjumlahan terdiri dari kombinasi penjumlahan 0 + 0 hingga 9 + 9.

Umumnya, peserta didik untuk pertama kalinya memperoleh pembelajaran tentang operasi hitung penjumlahan adalah pada kelas 1 Sekolah Dasar. Taraf berpikir mereka masih konkret. Karenanya, pembelajaran akan lebih mudah untuk dipahami apabila dilakukan dengan menggunakan benda-benda konkret atau alat peraga dan dikaitkan dengan kehidupan sehari-hari. Soal-soal cerita diubah terlebih ke dalam model konkret atau model diagram (gambar), kemudian baru dilanjutkan ke dalam bentuk simbol. Contohnya adalah sebagai berikut.

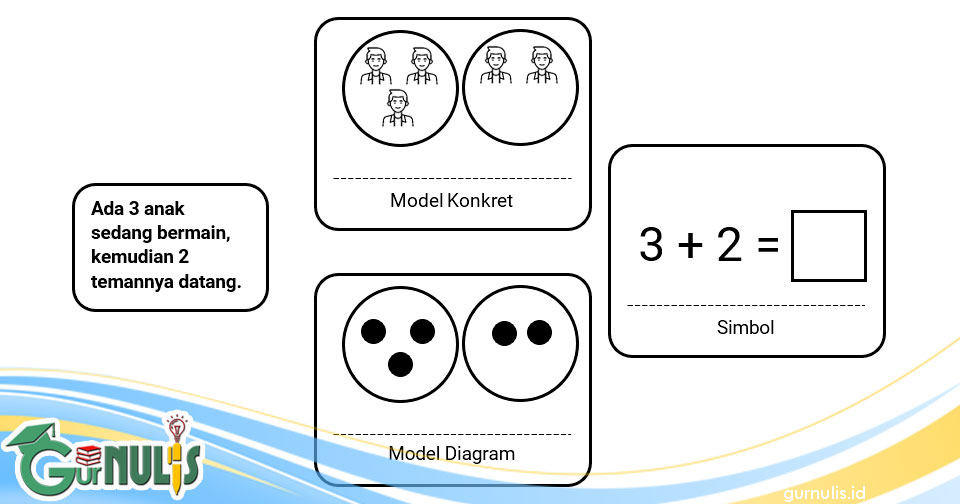
Ada 3 anak yang sedang bermain. Kemudian, 2 temannya datang bergabung. Ada berapa anak sekarang?

Soal cerita di atas dapat diterangkan kepada peserta didik melalui langkah-langkah pada gambar berikut.

Pada peserta didik Sekolah Dasar, ada 4 pendekatan atau jalan yang dapat digunakan untuk menerangkan penjumlahan, yaitu melalui kumpulan, melalui pengukuran, melalui mesin fungsi, dan melalui cara berusun (baik bersusun panjang maupun bersusun pendek).

Penjumlahan Bilangan Cacah melalui Kumpulan

Penjumlahan bilangan cacah melalui kumpulan didasarkan pada gabungan dua kumpulan lepas. Mengingat dunia peserta didik di Sekolah Dasar masih real, maka kumpulan yang diambil harus berupa kumpulan dengan anggota yang real atau bisa juga dengan gambar dengan anggota yang real. Contohnya adalah sebagai berikut.

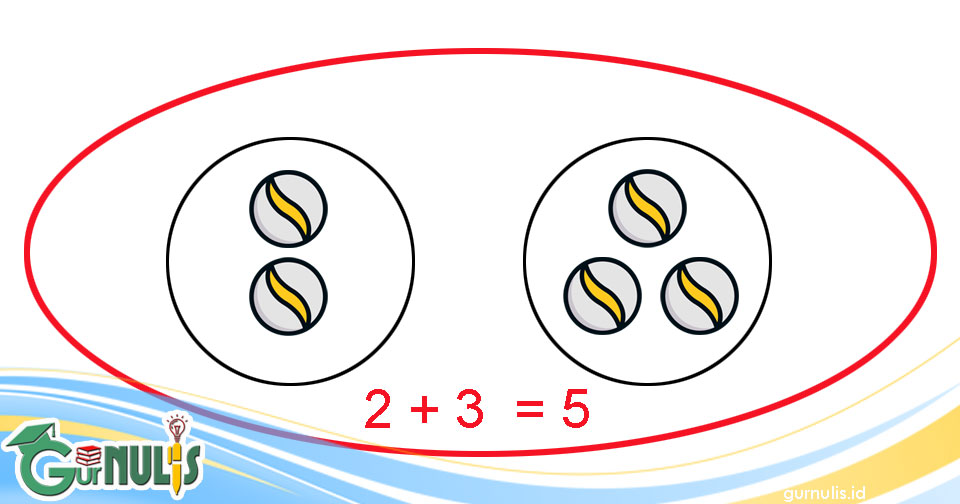
Saya mempunyai 2 buah kelereng. Saya membeli tiga buah kelereng lagi. Berapa buah kelereng yang sekarang saya miliki?

Pada saat kita menceritakan hal ini kepada peserta didik, kita sebaiknya membawa 5 buah kelereng dan seutas tali atau semacamnya untuk dijadikan batas kumpulan kira-kira seperti pada gambar berikut.

Catatan:
Kita dapat juga mengganti kelereng dalam soal cerita tersebut dengan menggunakan benda-benda lain, seperti mobil-mobilan, pensil, buku, dan lain-lain. Peserta didik hendaknya dilibatkan secara aktif dalam menyelesaikan soal tersebut. Misalnya guru mengawali dengan kata-kata sebagai berikut.

Ini, Bu Guru mempunyai 2 buah kelereng. Coba ambil 3 kelereng lagi yang Nak, gabungkan ke sini!

Setelah peserta didik mengambil lagi kelereng dan menggabungkannya, guru bertanya sebagai berikut.

Berapa banyaknya kelereng sekarang?

Contoh lain operasi hitung penjumlahan pada bilangan cacah dengan pendekatan kumpulan adalah sebagai berikut.

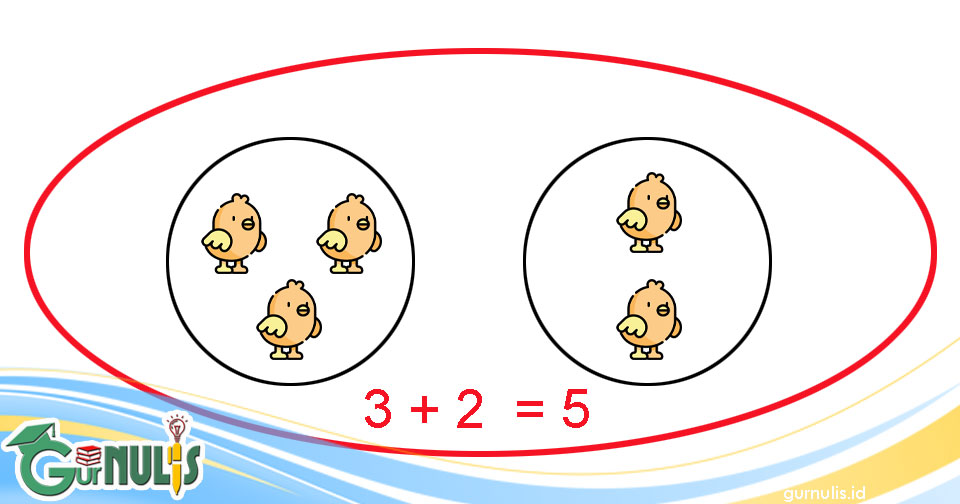
Di halaman rumah saya ada 3 ekor ayam. Tidak berapa lama datang 2 ekor ayam lagi. Ada berapa ekor ayam di halaman rumah saya sekarang?

Gambaran dari soal di atas adalah sebagai berikut.

Catatan:

Ayam bisa saja sukar untuk diadakan dan kalaupun ada kemungkinan untuk lepas sangatlah besar. Sebagai gantinya kita dapat menggunakan model ayam-ayaman.

Selain menggunakan model konkret yang berupa ayam dengan kumpulan seperti yang diterangkan di atas, guru dapat juga menggunakan papan flanel dengan gambar-gambar ayam (model ayam) ataupun yang lainnya yang dapat ditempelkan pada papan flanel tersebut. Peserta didik dapat aktif menjawab pertanyaan guru jika mereka menempelkan gambar ayam itu pada papan flanel. Pertanyaan-pertanyaan itu misalnya sebagai berikut.

Coba ambil 2 ekor ayam, kemudian tempelkan pada papan flanel tersebut. Ambil 3 ekor lagi dan tempelkan pada papan flanel lagi. Ada berapa ekor ayam sekarang?

Penjumlahan Bilangan Cacah melalui Pengukuran

Pada penjumlahan bilangan cacah melalui pengukuran, yang dijumlahkan itu bukan bilangan kardinal dari kumpulan-kumpulan, tetapi ukuran panjangnya. Penjumlahan dengan pengukuran dapat diperagakan dengan garis bilangan, timbangan (neraca) bilangan, ataupun dengan batang kuesioner berwarna. Berikut penjelasannya.

Penjumlahan melalui Garis Bilangan

Penjumlahan dengan garis bilangan yang dihitung adalah jaraknya, bukan jumlah titik-titik pada garisnya. Langkah-langkahnya adalah sebagai berikut.

Langkah pertamanya, guru memulai dengan keadaan real. Untuk itu, guru membuat garis bilangan pada lantai sebagai berikut.
Perintahnya misalnya sebagai berikut.
Bu Guru melompat 2 lompatan ke sebelah kanan dimulai dari titik nol (0). Kemudian ayo kamu lanjutkan lompatan Bu Guru sebanyak 3 langkah. Apa yang akan terjadi? Berapa langkah yang telah kita lakukan bersama?
Langkah keduanya, guru dapat menggunakan kertas bergaris bilangan yang ditempelkan pada dinding atau papan tulis. Sebagai pelompatnya, dapat dibuat gambar katak dari kertas yang digunting, ataupun dari model lainnya. Gambarannya adalah sebagai berikut.
Perintahnya misalnya sebagai berikut.
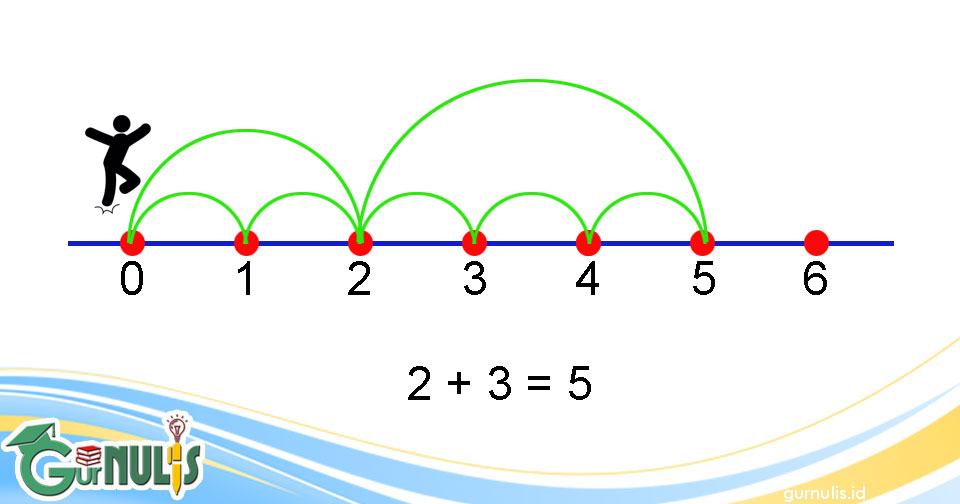
Coba ambil katakmu, Nak! Lompatkan katakmu 2 langkah ke kanan dengan dimulai dari nol (0) dan lompatkan dia 3 langkah lagi! Berapa langkahkah katakmu melompat? Jadi berapakah hasil dari 2 + 3?
Langkah ketiganya, setelah diperagakan dengan menggunakan benda-benda real dan modelnya, guru menggunakan model yang lebih abstrak, yaitu hanya dengan menggunakan garis bilangan. Gambarannya adalah sebagai berikut.

Penjumlahan melalui Timbangan (Neraca) Bilangan

Timbangan atau neraca dapat digunakan untuk memperagakan penjumlahan bilangan cacah. Contohnya adalah sebagai berikut.

Timbangan (neraca) digunakan untuk menunjukkan 2 + 3 = 5 atau 3 + 2 = 5. Cara menggunakan timbangan (neraca) penjumlahan adalah sebagai berikut.

Pada langkah pertama, ambil sekeping batu timbangan dan letakkan pada posisi 2.
Pada langkah kedua, ambil lagi sekeping batu timbangan dan letakkan pada lengan neraca yang sama namun pada posisi 3.
Pada langkah ketiga, agar timbangan ini seimbang, ambil lagi sekeping batu timbangan dan letakkan pada lengan neraca lainnya pada posisi 5. Ini menunjukkan bahwa 2 + 3 atau 3 + 2 adalah sama dengan 5. Perhatikan gambar berikut!

Penjumlahan melalui Batang Kuesioner Berwarna

Untuk melakukan penjumlahan dengan batang kuesioner berwarna, dapat ditempuh langkah-langkah berikut.

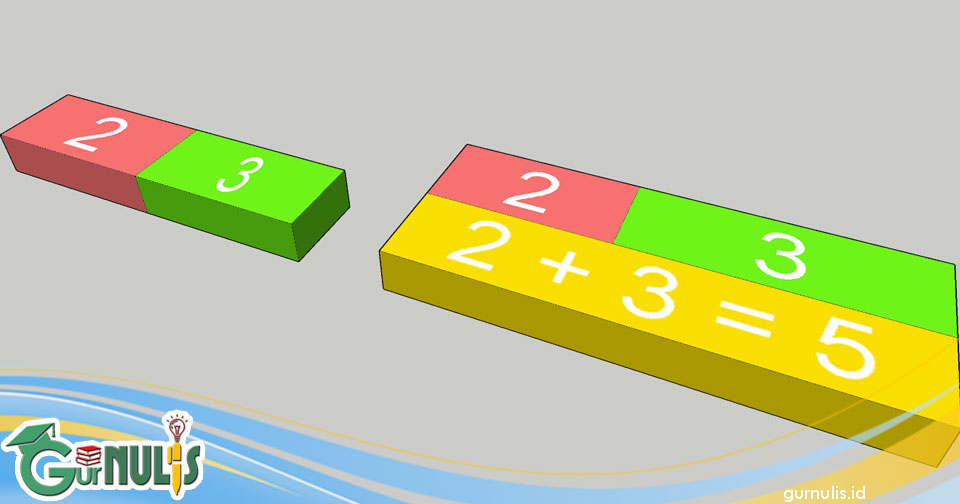
Ambil satu batang duaan, yaitu batang yang berwarna merah. Kemudian satu batang tigaan, yaitu batang yang berwarna hijau muda. Tempatkan kedua batang tersebu dengan ujung-ujungnya yang saling melekat.
Cari batang kuesioner lain yang dapat mentutup persis kedua batang tersebut. Anggap saja batang tersebut berwarna kuning. Panjang batang tersebut ternyata adalah 5 satuan. Ini artinya 2 + 3 = 5.

Penjumlahan melalui Mesin Fungsi

Umumnya, mesin fungsi tidak dipergunakan untuk menerangkan atau mengerjakan operasi hitung lainnya. Mesin fungsi ini lebih banyak digunakan untuk latihan pengenalan pada fungsi. Contoh penjumlahan melalui mesin fungsi adalah sebagai berikut.

Ambillah sebuah mesin fungsi, misalnya "+3". Pada muka kartu yang keluar, kita harus menulis lambang bilangan untuk bilangan tiga lebih besar dari bilangan yang dimasukkan. Misalnya apabila pada muka kartu yang dimasukkan itu tertulis 2, maka pada bagian belakangnya harus ditulis 5. Apabila pada muka kartu yang dimasukkan itu tertulis 6, maka pada bagian belakangnya harus ditulis 9, dan seterusnya. Gambarannya adalah sebagai berikut.

Ketika kartu bertuliskan 2 dimasukkan ke dalam mesin "+3" hasilnya akan berubah menjadi kartu bertuliskan 5.

Konstruksi dari mesin fungsi tersebut adalah sebagai berikut. Sahabat Pendidik boleh membuatnya.

Bilangan-bilangan yang tertulis pada kartu fungsi "+3" adalah:

masukan 1, hasilnya 4;
masukan 2, hasilnya 5;
masukan 3, hasilnya 6;
masukan 4, hasilnya 7;
masukan 5, hasilnya 8;
masukan 6, hasilnya 9;
masukan 7, hasilnya 10;
dan seterusnya.

Apabila bilangan yang dimasukkan tersebut dimisalkan x, maka hubungan antara yang masuk dan yang keluar tersebut adalah f : x → x + 3. Ini tidak lain adalah sebuah fungsi. Dengan kata lain, bila yang masuk kita misalkan x yang keluar kita misalkan y, maka hubungan antara x dan y adalah y = x + 3. Ini merupakan sebuah fungsi yang berbentuk linier.

Penjumlahan Bilangan Cacah melalui Cara Bersusun Panjang dan Cara Bersusun Pendek

Penjumlahan bilangan cacah yang ditempuh dengan cara bersusun. Contoh penyelesaian soal ceritanya adalah sebagai berikut.

Pak Agus mempunyai kebun kelapa. Pada bulan Januari ia memetik 2.438 buah. Pada bulan Februari ia memetik 1.562 buah. Pada bulan Maret ia memetik 3.724 buah. Berapa jumlah buah kelapa yang dipetik selama tiga bulan tersebut?

Soal tersebut dapat diselesaikan dengan cara bersusun panjang maupun dengan cara bersusun pendek.

Penyelesaian Penjumlahan dengan Cara Bersusun Panjang

Penjumlahan dengan cara bersusun panjang ditempuh dengan menguraikan setiap bilangan sesuai dengan nilai tempatnya sebagai berikut.

Perhatikan penguraian-penguraian bilangan di atas sebagai berikut.

2.438 = 2.000 + 400 + 30 + 8;
1.562 = 1.000 + 500 + 60 + 2;
3.724 = 3.000 + 700 + 20 + 4.

Penyelesaian Penjumlahan dengan Cara Bersusun Pendek

Penjumlahan bilangan dengan cara bersusun pendek dilakukan berdasarkan nilai tempat dengan sistem menyimpan sebagai berikut.

Langkah-langkah penyelesaiannya adalah sebagai berikut.

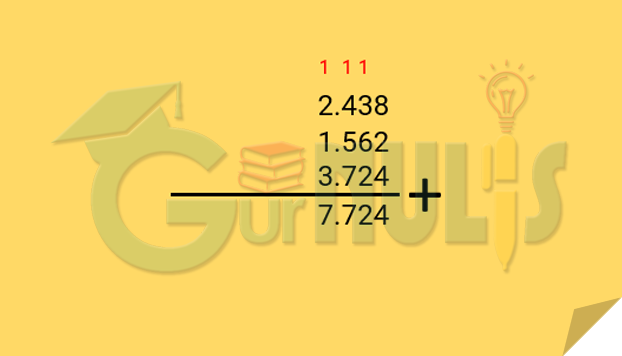
Jumlahkan nilai tempat satuan 8 + 2 + 4 hingga menghasilkan 14. Tulis 4, simpan 1 pada tempat puluhan.
Jumlahkan nilai tempat puluhan 1 (simpanan tadi) + 3 + 6 + 2 hingga menghasilkan 12. Tulis 2, simpan 1 pada tempat ratusan.
Jumlahkan nilai tempat ratusan 1 (simpanan tadi) + 4 + 5 + 7 hingga menghasilkan 17. Tulis 7, simpan 1 pada tempat ribuan.
Jumlahkan nilai tempat ribuan 1 (simpanan tadi) + 2 + 1 + 3 hingga menghasilkan 7. Tulis 7.
Dari hasil penyelesaian tersebut didapatkan bahwa 2.438 + 1.562 + 3.724 = 7.724.

Sifat-sifat Penjumlahan Bilangan Cacah

Sifat-sifat penjumlahan bilangan cacah terdiri dari sifat tertutup dan sifat pertukaran (komutatif). Pada tahap ini, guru di Sekolah Dasar cukup memahamkan sifat-sifat ini pada bilangan cacah sederhana.

Sifat Tertutup pada Penjumlahan Bilangan Cacah

Sifat tertutup pada bilangan cacah maksudnya apabila dua bilangan cacah dijumlahkan, maka hasilnya adalah bilangan cacah pula. Contohnya apabila diambil dua bilangan cacah, 3 dan 6 misalnya. Apakah hasil penjumlahan dari keduanya adalah bilangan cacah? Ya, tepat, 9 adalah bilangan cacah! Sifat tertutup ini hanya berlaku pada penjumlahan bilangan cacah saja dan tidak berlaku pada pengurangan bilangan cacah.

Sifat Pertukaran pada Penjumlahan Bilangan Cacah

Sifat pertukaran pada bilangan cacah maksudnya setiap dua bilangan cacah sembarang apabila dijumlahkan letaknya selalu dapat dipertukarkan. Ini dikatakan bahwa penjumlahan pada bilangan cacah memenuhi sifat komutatif. Contohnya apabila diambil dua bilangan cacah, 3 dan 6 misalnya. Apakah 3 + 6 = 6 + 3? Ya, tepat, jawabannya adalah sama, yaitu 9! Baik 3 maupun 6, walaupun letaknya saling ditukarkan, hasil penjumlahannya adalah sama. Sifat pertukaran ini hanya berlaku pada penjumlahan bilangan cacah, tidak dengan pengurangan bilangan cacah.

Kebenaran dari sifat pertukaran ini dapat diperagakan secara konkret dengan media himpunan, kartu nilai tempat, blok model Dienes, garis bilangan, timbangan (neraca) bilangan, batang kuesioner, kantong nilai tempat, dan abakus.

Demikianlah bahasan mengenai operasi penjumlahan pada bilangan cacah, ya Sahabat Pendidik. Semoga bahasan mengenai fakta-fakta penjumlahan, pendekatan penjumlahan, dan sifat-sifat penjumlahannya bermanfaat.

Salam litersi guru ndeso.

Munasifatut Thoifah

Guru yang selalu ingin berbagi inspirasi.

Iklan Header